.png&blockId=7628ec0c-1357-4c37-a1e9-32a282f6efaa)
.png&blockId=5d4e07f0-899e-4a0b-b753-19c9d3356b47)
.png&blockId=5d4e07f0-899e-4a0b-b753-19c9d3356b47&width=256)
.png&blockId=be06ed4d-0152-4f0f-b4b4-821bd1fb30d9)
.png&blockId=39a86e12-3cf4-40df-8d5e-9891c5adc274)
_%25E1%2584%2587%25E1%2585%25A9%25E1%2586%25A8%25E1%2584%2589%25E1%2585%25A1%25E1%2584%2587%25E1%2585%25A9%25E1%2586%25AB.png&blockId=891e6648-1148-4e7c-bfcd-0463dc71545c)
.png&blockId=5e737e69-4f36-437b-95e0-7db747173000)
.png&blockId=5294c22e-8cee-4109-963f-c8cfe8c852cf)
문제 - 839. Similar String Groups
문제에는 해당 그림 X(내가 그린 그림)
•
Two strings X and Y are similar if we can swap two letters (in different positions) of X, so that it equals Y. Also two strings X and Y are similar if they are equal.
•
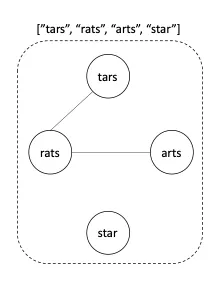
For example, "tars" and "rats" are similar (swapping at positions 0 and 2), and "rats" and "arts" are similar, but "star" is not similar to "tars", "rats", or "arts".
•
Together, these form two connected groups by similarity: {"tars", "rats", "arts"} and {"star"}. Notice that "tars" and "arts" are in the same group even though they are not similar. Formally, each group is such that a word is in the group if and only if it is similar to at least one other word in the group.
•
We are given a list strs of strings where every string in strs is an anagram of every other string in strs. How many groups are there?
해석
•
두개의 문자열 X와 Y가 있다. 이 때, X와 Y가 같거나, 문자 2개의 위치를 바꾸었을 때 X와 Y가 같아진다면 Similar라고 본다.
◦
한국에서 숫자 야구라는 게임을 보면 문자와 문자 순서가 같다면 Strike, 문자는 맞지만 순서가 다르다면 Ball이라고 한다.
예) 1234 → 2134 : 2 Ball 2 Strike
◦
즉, 위 게임을 예로 들어보면 문자열의 길이가 N이라고 했을 때, N Strike 혹은 2 Ball N-2 Strike일 경우에 Similar라고 본다.
•
이 때 Similar끼리 그룹을 짓는데 tars와 rats는 similar, tars와 arts는 Not similar, arts와 rats는 simalar다. 이렇게 하나의 그룹 안에서 Similar가 존재한다면 그 또한 Similar로 본다.
◦
즉, tars와 arts는 similar가 아니지만 tars와 rats는 similar이기 때문에 tars, rats, arts는 하나의 그룹으로 본다.
•
마지막으로 몇개의 Similar 그룹이 생성되는지 구해라.
첫 로직 : DP - LinkedList
처음에는 DP와 LikedList로 문제를 풀고자 하였다. 하지만, for문이 굉장히 많이 나오게 되면서 시간 복잡도가 현저히 낮아지게 되었다.
또한 내가 짠 로직은 아래와 같다.
if 2자리만 다르거나 문자열이 같은지 Check
if Similar라면 해당 문자열들을 LinkedList에 추가
if 만들어진 LinkedList 외의 다른 LinkedList에도 포함될 수 있는지 확인
포함될 수 있다면 LinkedList 이어주기
else 아니면 새로운 LinkedList의 root Node로 생성
위 로직은 틀리지는 않았지만, 모든 문자열과, 모든 Node들을 하나하나 다 탐색해야 하기 때문에 시간이 어어어엄청 오래걸리고, 만약 입력 받은 strs가 매우 크다면 메모리 효율도 굉장히 떨어지게 된다.
DP 외의 다른 방법으로 풀고자 하였으나, 부족한 알고리즘 지식으로 푸는데 한계를 느껴 Solution 참고…….
Solution을 보고 푼 코드
UF = {}
def find(val):
if val not in UF:
UF[val] = val
elif UF[val] != val:
UF[val] = find(UF[val])
return UF[val]
def union(val1, val2):
rootX = find(val1)
rootY = find(val2)
UF[rootX] = rootY
def is_similar(val1, val2):
if val1 == val2:
return True
diff = 0
for i in range(len(val1)):
if val1[i] != val2[i]:
diff +=1
return diff == 2
class Solution:
def numSimilarGroups(self, strs: List[str]) -> int:
for i in range(len(strs)):
for j in range(i+1, len(strs)):
if is_similar(strs[i], strs[j]):
union(strs[i], strs[j])
return len(set(find(val) for val in strs))
Python
복사
•
Solution을 보니 DFS, BFS로 푼 사람들이 굉장히 많아 내 로직이 틀린줄 알았지만, Union-Find라는 알고리즘으로 푼 사람들도 있었다. Union-Find라는 개념은 노드를 합치는 Union연산과 노드의 루트 노드를 찾는 Find연산으로 이루어져 있다.
•
찾아보니 학교 수업시간에서 배웠던 알고리즘이다…….
•
내가 처음 생각한 로직을 DP로 짯을 때보다 for문이 2개나 줄었다….
Union-Find 알고리즘
•
그래프 알고리즘으로 두 노드가 같은 그래프에 속하는지 판별
•
서로소 집합, 상호 베타적 집합(Disjoint-Set)으로도 불린다
설명
2개의 예제로 설명해보겠다.
위 문제와 같은 예제 - [”tars”, “rats”, “arts”, “star”]
1.
비교 순서는 2개의 for문으로 tars-rats, tars-arts, rats-arts, arts-star로 버블 정렬의 순서와 같다.
2.
is_similar() 함수를 통해 Similar인지 판별한다.
3.
만약 Similar라면 union()으로 들어간다.
여기서부터 순서대로 해보겠다.
tars-rats
•
Similar이기 때문에 union으로 들어간다.
•
여기서 union() 로직을 살펴보자
◦
find()로직을 통해 tars의 root는 tars가 나오고 rats의 root는 rats가 나오게 된다.
◦
이후 union() 에 의해 UF[tars] : rats가 되기 때문에 UF = {tars : rats, rats : rats} 가 된다.
tars-arts
•
Similar가 아니기 때문에 Pass
rats-arts
•
Similar이기 때문에 union으로 들어간다.
•
여기서 union() 로직을 살펴보자
◦
find()로직을 통해 rats의 root는 rats가 나오고 arts의 root는 arts가 나오게 된다.
◦
이후 union() 에 의해 UF[rats] : arts가 되기 때문에 UF = {tars : rats, rats : arts, arts : arts} 가 된다.
arts-star
•
Similar가 아니기 때문에 Pass
어? 그럼 UF에는 1개만 들어가게 되는거 아닌가요? 라고 할 수 있지만, group의 개수는 마지막 return 로직에 의해 결정된다.
strs에 있는 모든 문자열에 대해서 Root Node를 찾는 find()를 실행해준 후 set을 이용해 중복을 제거해준다. 이를 통해 group의 개수를 알 수 있게 된다.
이 때 set으로 중복 제거하기 전 list는 [arts, arts, arts, star]가 될 것이다.
위 문제에 중복을 추가한 예제 - [”tars”, “rats”, “arts”, “star”, “stra”, “sart”]
여기서는 Similar가 되는 부분만 살펴보겠다.
tars-rats
•
find()로직을 통해 tars의 root는 tars가 나오고 rats의 root는 rats가 나오게 된다.
•
이후 union() 에 의해 UF[tars] : rats가 되기 때문에 UF = {tars : rats, rats : rats} 가 된다.
tars-sart
•
find()로직을 통해 tars의 root는 rats가 나오고 sart의 root는 sart가 나오게 된다.
•
이후 union() 에 의해 UF[rats] : sart가 되기 때문에 UF = {tars : rats, rats : sart, sart : sart} 가 된다.
rats-arts
•
find()로직을 통해 rats의 root는 sart가 나오고 arts의 root는 arts가 나오게 된다.
•
이후 union() 에 의해 UF[sart] : arts가 되기 때문에 UF = {tars : rats, rats : sart, sart : arts, arts : arts} 가 된다.
star-stra
•
find()로직을 통해 star의 root는 star가 나오고 arts의 root는 stra가 나오게 된다.
•
이후 union() 에 의해 UF[star] : stra가 되기 때문에 UF = {tars : rats, rats : sart, sart : arts, arts : arts, star : stra, stra : stra} 가 된다.
stra-sart
•
find()로직을 통해 stra의 root는 stra가 나오고 sart의 root는 arts가 나오게 된다.
•
이후 union() 에 의해 UF[stra] : arts가 되기 때문에 UF = {tars : rats, rats : sart, sart : arts, arts : arts, star : stra, stra : arts} 가 된다.